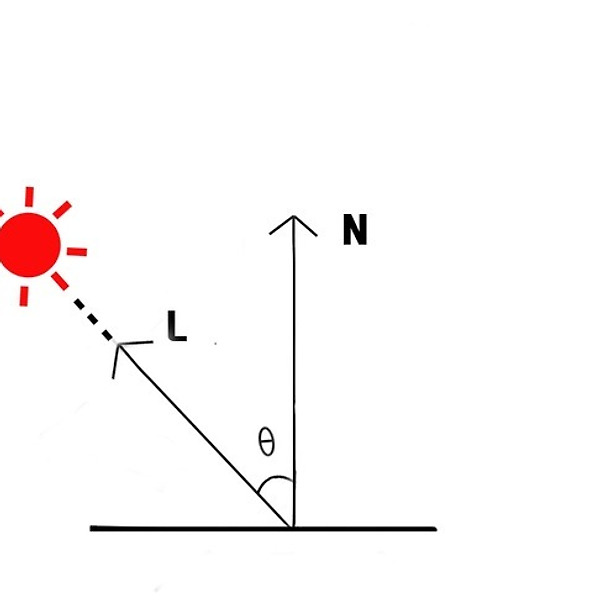
Shadow Mapping
Posted by Go crazy for anything that will make you smile.
Depth Shadow(깊이 그림자), Shadow Maps(그림자 맵), Depth Bufffer Shadow(깊이버퍼 그림자) 등의 여러가지 이름으로 불린다. 이 기법의 핵심은 광원으로부터 물체까지의 거리정보를 저장해서 사용한다는 것이다. 1. depth 찍기 // 조명위치로 시선 이동 float3 vLook = float3(0,0,0); float3 vEye = lightPos.xyz; float3 vUp = float3(0,0,1); // 조명의 시야벡터들 만들고 뷰 공간으로 변환 float4x4 lightMat = GenViewMatrix(vLook, vEye, vUp); Pos -= lightPos; Out.Pos = mul(Pos, lightMat); // 조명의 투영변환행렬. Out.Pos..