ray casting을 이해해 보자..
목표 ray를 이해하고 구현해보자.
ray(광선) casting(투사)는 무었인가?
레이캐스팅에 대해 알기 위해서는 이 기술의 탄생 배경을 좀 살펴봐야 한다.
GI(전역 조명모델)와 LI(지역 조명모델)을 보면 GI의 경우 다른 물체면에서 반사되어 입사하는 빛까지 고려한
조명모델이며 LI는 광원으로부터 직접 물체면으로 입사되는 빛만을 고려한 모델이다.
보다 사실적인 화면을 얻기 위해서는 전역조명 모델을 적용하고자 하였으며
그 시도중 하나가 레이캐스팅이다.
단순히 카메라(관찰자)로부터 광선이 출발한다고 하고, 결과적으로 이 빛의 진행 경로를 막고 있는 가장 가까운
물체를 찾는 것이다.
레이캐스팅은 정확하게 말하자면 전역조명을 위한 것은 아니고 가시면 검출을 위한 것이다.
카메라 시점에서 광선을 한번 던진 다음에 물체와 교차점 검수만 수행하기 때문에 실제적으로 이 광선이
다른 물체에 영향을 끼치진 않는다.
즉, 각 픽셀로부터 가장 가까운 물체에 이르는 단일 광선을 고려한다.
https://celdee.tistory.com/587
Global Illumination : Ray Casting and Ray Tracing
지역 조명 모델에서는 광원에서 빛이 방출되고, 표면에 충돌했을 때 관찰자에게 빛이 도달할 때까지 다른 빛의 영향을 받지 않는 것으로 가정한다. 하지만, 실제 자연 현상은 이보다 복잡하다.
celdee.tistory.com
ray(광선) Tracing(추적)는 무었인가?
레이 캐스팅고 같이 레이를 쏘는데 물체의 표면에 닿은 후 현실에서 처럼
빛이 다시 재귀적으로 반사되어 결과물을 렌더링 하는 방식이다.
레이캐스팅과의 가장 큰 차이점은 레이 트레이싱은 일회성인 반면에 레이트레이싱은
계속해서 빛을 반사시켜 어디에 부딪히는지를 추적하는 방식이다.
여기서는 레이 캐스팅이나 레이트레이싱에 대한 논의 보다 레이를 쏘는 것에 대한
실질적 구현에 대해 서술하고자 하기에 간단한 레이캐스팅을 예로 개념을 이해해 보자.
레이캐스팅을 구현하는 과정을 개념적으로 이해해 보자.
일련의 과정.

빛의 경로를 광원 -> 물체 -> 카메라 가 아니라 반대로 카메라 -> 물체 -> 광원 방식의 역추적.
역추적은 눈(카메라)에서 이미지평면의 각 픽셀 중심을 통과하는 추적광선으로 구성된다.
위 이미지로부터 알 수 있는것.
- 레이(광선)들은 항상 카메라 원점(camera origin)에서 시작한다.

내용을 단순화 하기 위해 렌더링된 이미지(이미지 평면)는 그냥 가로 세로가 같은 정사각형이라고 가정한다.
왼쪽 이미지 : 이미지 평면 크기는 6x6 픽셀이며 카메라(eye)의 기본 위치는 월드의 중심인(0,0,0).
카메라가 -z축을 따라 어떻게 가리키는지 확인. 이미지 평면은 원점에서 정확히 1 (임의 설정)떨어져 있다.
첨언 : z축 방향은 사용하는 그래픽 api에 따라 다르다. opengl이나 dx가 다른것 처럼. 여기서는 opengl을 따름
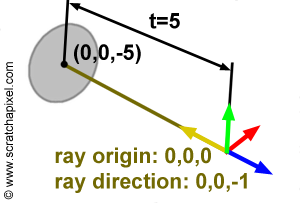
레이와 구의 교차(레이 히트)
위 그림 1에서처럼 픽셀 중앙의 점의 위치를 계산하기 위해, 원래 raster space로 표현되었던 픽셀 좌표를
world로 변환하는 작업이 필요하다.
screen space-> ndc -> raster space 설명은 아래 "더보기"

픽셀로 표시되는 컴퓨터 화면에 출력하기 위해서는 켄버스 위의 점의 좌표는
screen space(실수)에서 NDC space(실수)를 거쳐 raster space(정수)로 변환해야 한다.
https://blog.naver.com/likejuststarted/222722312905
Screen space 에서 Raster space로 변환
1. 좌표 시스템 (Screen space -> NDC space -> Raster space) Pixel로 표시되는 컴퓨터 화면...
blog.naver.com
world space는 기본적으로 장면의 모든 객체, 지오메트리, 라이팅 및 카메라의 좌표가 표현되는 공간이다.
예를들어 구가 음의 z축을 따라 5단위 떨어져 있는 경우 월드 공간 좌표는 (0,0,-5)다.
이 구와 광선의 교차점을 계산을 위해 수학공식을 적용하려면 광선의 원점과 방향도 같은 공간으로 정의되야 한다.
예를들어 광선의 원점(0,0,0)과 방향(0,0,-1)이 있고 이 값이 월드 공간 좌표계의 좌표를 나타내는 경우
광선은 (0,0,-5)에서 교차하며 이러한 예시가 그림 3에 나와있다.

raster 에서 screen space로.
참고 링크 : Computing the Pixel Coordinates of a 3D point.
알고 있는 것 활용 :
이미지 평면이 world space의 원점에서 정확히 1 단위 떨어진 곳에 위치하고(가정), 음의 z축을 따라 정렬되어 있다.
이미지가 정 사각형이므로 이미지가 투영되는 이미지 평면의 부분도 정사각형.
이 projection영역의 크기는 2x2(그림 2 참고)
또한 raster 이미지가 픽셀로 구성되어 있음을 알고 있음.
우리가 필요로 하는것은 raster space에서 이들 픽셀의 좌표와 동일한 픽셀의 좌표 사이에서 world space로
표현되는 관계를 찾는것.

픽셀 중간에 있는 점의 좌표를 표준 좌표로 변환하려면 몇가지 단계가 필요하다.
이 점의 좌표는 먼저 raster space(오프셋 0.5를 더한 픽셀 좌표)로 표현 한 다음,
NDC space로 변환(좌표를 0~1범위로 리매핑)한 다음,
Screen space로 변환(NDC 좌표를 -1~1범위로 리매핑)한다.
NDC 공간에서 Screen 공간으로 리매핑 하기 위해 (x,y)*2-1 해준후 y축은 -1을 곱해준다.
이는 위 그림5를 보면 알 수 있음.
최종 카메라 -> world 변환 4x4 행렬을 적용하면 Screen space의 좌표가 world space로 변환된다.
자세한 설명은 아래 "더보기"
첫번째로 프레임차원에서 픽셀 위치를 정규화 시켜야 한다.
픽셀들의 정규화 된 새 좌표를 NDC Space에 정의되었다 라고 말한다.
NDC space :
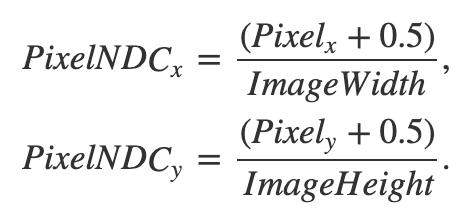
최종 카메라 레이가 픽셀의 정중앙을 지나길 원하기 때문에 픽셀에 약간의 이동(0.5)를 준다는 것을 기억해야 한다.
NDC 공간으로 표현된 픽셀 좌표는 0~1범위에 있다.
(레이트레이싱에서의 NDC 공간은, Rasterization World의 NDC 공간[일반적으로 -1~1범위로 매핑됨]과 다르다.)
그림 2에서 볼 수 있듯이, 이미지 평면은 world의 원점을 중심으로 한다.
다시 말해 이미지 왼쪽에 있는 픽셀은 음의 x좌표를 가져야 하고, 오른쪽에 있는 픽셀은 양의 x좌표를 가져야 한다.
동일한 논리가 y축에 적용된다.
y축으로 정의된 선보다 위쪽에 있는 픽셀은 양의 y좌표를 가지고, 아래쪽에 있는 픽셀은 음의y좌표를 가진다.
현재 [0:1]인 NDC 좌표를 [-1:1] 범위에 있는 정규환 된 픽셀좌표를 다시 매핑하여 이 문제를 보정할 수 있다.
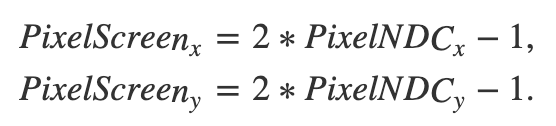
그런데 이 방식을 사용하면 리매핑된 y는 기호가 반대가 된다.
위 그림5 처럼 y 부호가 정해지려면 y는 다른방식의 연산을 사용해야 한다.

첨언 : 아니면 그냥 y부호만 뒤집어 주던지.
이렇게 screen space에 정의된 좌표값을 얻게 되었는데 처음에 이미지가
정사각형이라고 가정했었기 때문에 종횡비(aspect ratio)를 구하는 방법은 꽤 간단하다.
이미지 크기가 7x5 픽셀인 경우를 보면(작은 이미지이긴 하지만 그래도 이미지임) width를 height로 나누면
7/5가 되기 때문에 1.4가 된다.
픽셀 좌표가 screen space에 정의되면 범위는 -1~1 범위에 있기 때문에 x축이 더 많은 픽셀(7)이 있고
y축이 더 적은 픽셀(5)이 있기 때문에 결국 픽셀은 세로축을 따라 찌그러지고 늘어난다.

그림 6의 왼쪽 그림은 정사각형인데 픽셀수가 다르기 때문에 픽셀이 정사각형이 아니다.
이를 수정하기 위해 너비를 이미지의 높이로 나누어 계산할 수 있는
이미지 종횡비로 x축을 따라 이미지 평면을 보정해야 한다.
픽셀을 다시 정사각형으로 만들려면 (픽셀을 픽셀답게) 픽셀의 x좌표에 이미지 종황비(화면비율)을 곱해야 한다.
그림6을 참고했을때 이 경우는 현재 1.4다.
screen space 에서 y픽셀 좌표를 변경하지 않은 상태로 둔다는 것을 숙지해야 한다.
이는 y픽셀이 여전히 -1~1범위에 있지만 x픽셀은 이제 -1.4~1.4 범위에 있기 때문이다.


위 이미지는 카메라 세팅의 측면도.
카메라(눈) 위치에서 이미지 평면까지의 거리는 1 단위(벡터 AB)
B에서 C까지의 거리도 1단위.
간단한 삼각범을 이용해서 a의 각도를 쉽게 계산할 수 있다.
FOV 계산을 살펴보자.
지금까지 screen space에 정의된 점의 y좌표는 -1~1범위에 있다.
또한 이미지 평면이 카메라 원점에서 1 단위 떨어져 있다는 것도 알고 있다.
우리가 알고있는 정보(카메라 위치, 오브젝트의 위치)등으로 레이의 위치와 방향을 정의하기 위해서는
우리가 알고 있는 정보와 공간을 맞춰서(월드공간) 계산해야 한다.

이 공식을 이용해서 a/2 (그림 7)값을 구해보자.
(위 삼각함수에서는 A 각도, 그림 7에서는 a/2. 이미지가 달라서 지칭 용어가 다름)

그림 7에서 구하고자 하는 값인 a/2는 arctan(높이/밑변)인데 여기서는 카메라와 이미지 평면의 거리를
1로 가정했고 이미지 평면은 -1~1범위(즉 높이가 2)이니까 절반값인 B에서 C까지의 거리도 1.
그러면 결국 위 공식과 같은 결과가 나온다.
파이 라디안이 180도니까 위 공식에서 a의 결과는 90라디안.
즉, 특정 경우(카메라와 이미지 평면거리를 1이라 가정하고, y가 -1~1로 알고있을경우)의 각도 a는 90도이다.

BC의 길이를 계산하려면 각도a의 접선을 2로 나눈 값만 계산하면 된다.
첨언 : tan(a/2)의 값은 높이/밑변 인 BC / AB 인데 AB가 1이니까 BC를 구하려면 그냥
tan(a/2)만 구하면 된다는 뜻인듯. 이 경우에 한해서만.

a가 90보다 크면 BC의 길이는 1보다 크고 (110이면 tan(110/2)는 tan(55)이고 이 값은 1보다 크다)
a가 90보다 작으면 BC의 길이는 1보다 작다는 것을 기억하자. (60이면 tan(60/2)이고 tan(30)은 1보다 작다)
따라서 이 숫자를 스크린 픽셀 좌표(현재는 -1~1)에 곱해서 확대 또는 축소를 할 수 있다.
짐작할 수 있듯이 이 작업은 우리가 보는 장면의 양을 변경한다.
이 작업은 줌인(화각감소 = 보이는 장면 감소) 및 줌 아웃(화각 증가 = 보이는 장면 증가)과 같다.
결론적으로 우리는 화각(카메라의 시야)를 다음 것들로 표현해 정의할 수 있다.
각도 a의 탄젠트 값을 2로 나눈 결과를 스크린 픽셀좌표
(이 각도가 각도법(degree)로 표시되는 경우 호도법(radians)로 변환해야 함)와 곱한 값.

이 시점에서, 원래의 픽셀 좌표는 카메라의 이미지 평면과 관련하여 표현된다.
1. 정규화 되고
2. -1~1사이로 리매핑 되고
3. 이미지 종횡비에 의해 곱해지고
4. 시야각 a의 탄젠트를 2로 나눈값에 의해 곱해진다.
이 점은 카메라 좌표계와 관련하여 표현되기 때문에 camera space에 있다고 말한다.
카메라가 기본위치에 있으면, 카메라의 좌표계와 world의 좌표계가 일렬로 정렬된다.
이 점은 카메라 원점에서 1 단위 떨어진 이미지 평면에 있지만, 카메라 역시 음의 z축을 따라 정렬되 있다는 의미다.
따라서 이미지 평면에서 픽셀의 최종 좌표를 다음과 같이 표현할 수 있다.

이를 통해 카메라의 이미지 평면위에 있는 이미지의 픽셀의 위치 P를 얻을 수 있다.
여기에서 광선의 원점을 카메라의 원점(O)로 정의하고
광선의 방향을 정규화된 벡터 OP로 정의하여 이 픽셀의 광선을 계산할 수 있다(그림 8)
벡터 OP는 단순히 이미지 평면에서 카메라 원점을 뺀 지점의 위치다.
카메라가 기본 위치에 있을 때 카메라 원점과 월드 좌표계는 동일하므로 점 O는 단순히 0,0,0이다.
의사코드는 아래와 같다.
float imageAspectRatio = imageWidth / (float)imageHeight; // width > height 인 걸로 가정하고
float Px = (2 * ((x + 0.5) / imageWidth) - 1) * tan(fov / 2 * M_PI / 180) * imageAspectRatio;
float Py = (1 - 2 * ((y + 0.5) / imageHeight) * tan(fov / 2 * M_PI / 180);
Vec3f rayOrigin(0);
Vec3f rayDirection = Vec3f(Px, Py, -1) - rayOrigin; // 이거는 Vec3f(Px, Py, -1);랑 똑같은 거임!
rayDirection = normalize(rayDirection); // 이건 방향이니까 정규화 까먹지 말기
카메라의 최종 위치와 방향(orientation)은 일반적으로 카메라에서 world로 변환 행렬로 나타낼 수 있다.
O(카메라 원점이자 world좌표계의 원점)와 P(선이 통과하는 픽셀의 world 공간 위치)를 알고 있으면
camera to world 행렬에 의한 O와 P를 곱하면 O'와 P'를 쉽게 얻을 수 있다.
마지막으로 광선 방향은 P'-O'로 계산될 수 있다.
마지막으로, 특정 시점에서 장면 이미지를 렌더링 할 수 있기를 원한다.
카메라를 원래 위치(world 좌표계의 중심에 위치하고 음의 z축을 따라 정렬)에서 이동 한 후,
4x4 행렬로 카메라의 변환 및 회전값을 표현할 수 있다.
일반적으로 이 행렬을 camera to world행렬이라 하며 반대는 world to camera 행렬이라고 한다.
이 camera to world행렬을 점 O와 P에 적용하면 벡터 ||O'P'||는 (여기서 O'와 P'는 각각
camera to world 행렬에 의해 변환된 점 O와 점 P임) world공간에서 광선의 정규화 된 방향을 나타낸다.(그림8)
camera to world변환을 O와 P에 적용하면, 이 두 점은 카메라 공간에서 world 공간으로 변환된다.
float imageAspectRatio = imageWidth / imageHeight; // assuming width > height
float Px = (2 * ((x + 0.5) / imageWidth) - 1) * tan(fov / 2 * M_PI / 180) * imageAspectRatio;
float Py = (1 - 2 * ((y + 0.5) / imageHeight) * tan(fov / 2 * M_PI / 180);
Vec3f rayOrigin = Point3(0, 0, 0);
Matrix44f cameraToWorld;
cameraToWorld.set(...); // 매트릭스 설정하기
Vec3f rayOriginWorld, rayPWorld;
cameraToWorld.multVectMatrix(rayOrigin, rayOriginWorld);
cameraToWorld.multVectMatrix(Vec3f(Px, Py, -1), rayPWorld);
Vec3f rayDirection = rayPWorld - rayOriginWorld;
rayDirection.normalize(); // 이건 방향이니까 정규화 까먹지 말기최종 이미지를 계산하려면 방금 설명한 방법을 사용해서 프레임의 각 픽셀에 대해 광선을 만들고
이런 광선들이 장면의 형상과 교차하는지 테스트 해야 한다.
소스코드.
이미지의 각 픽셀에 광선을 생성하는 방법의 한 예시임.
간단하게 레이캐스팅 구현해 보기.
참고 : https://www.shadertoy.com/view/lssyD4
Shadertoy
www.shadertoy.com
구현내용
1. 미리 정의하는 내용들
: 카메라의 위치/타겟/FOV, 구의 위치/반지름.
2. 레이를 만든다. (레이는 위치와 방향)
- 위 설명의 그림 7에서 카메라의 위치A(0,0,0)에서 이미지 평면까지의 거리(focal) B를 계산한다.
focal = 1 / tan(radians(fov Y/2))
위 공식의 자세한 풀이는 아래 더보기 참고
현재 카메라 위치를 A, 이미지 평면의 위치를 C 라고 하면 카메라에서 이미지 평면과의 거리(focal) b로 생각할 수 있다.
그럼 tanA = a/b 이 공식에서 양 변을 a로 나눈후 역변하면.
=> b = a / tanA
그런데 ndc 특성상 a 크기는 1 이니까 b = 1/tanA 이다.
tanA값인 A를 아까 임의로 80도로 설정해 뒀는데 이를 라디안으로 바꾸면
b = 1 / tan(40 * 3.14 / 180) // fov를 80으로 했으니 여기서 A를 구하려면 절반인 40으로 해야 함.
| rad to degree | degree to radian |
| rad x 180 / π = 도(°) | 도(°) x π / 180 = radian |
이러한 계산으로 아래와 같은 공식이 나온다.
float focal = 1.0 / tan(radians(cameraFovY) / 2.0);
이렇게 초점거리를 구할 수 있었다.
- 월드 공간에서 X,Y,Z로 표시되는 세개의 카메라 메인 축들을 계산해야 한다.
그림7에서의 A(카메라위치)에서 B(카메라 target)로의 단위 방향 벡터(LookAt이라고 하자)를 만든다.
(카메라에서 타겟을 바라보는 방향. glLookAt)
AtoB = normalize(camera target - camera pos)
- LookAt을 만들고 UpVector을 (0,1,0)이라고 한 다음 이 두 벡터를 외적하여 두 벡터에 직교하는 벡터를 만든다.
(첨언 : 외적 결과는 무조건 오른손 법칙. 애초에 외적의 방향이 오른손 법칙을 만족하도록 정의됨)
참고 : https://jjycjnmath.tistory.com/482
외적(cross product)과 오른손 법칙(right hand rule)
$\R^3$의 두 벡터 ${\bf u} = (u_1,\, u_2,\, u_3)$와 ${\bf v} = (v_1,\, v_2,\, v_3)$에 대하여 ${\bf u}$와 ${\bf v}$의 외적(cross product) ${\bf u} \times {\bf v}$를 다음과 같이 정의한다.\[ {\bf u} \times {\bf v} = (u_2v_3 - u_3v_2,\, u
jjycjnmath.tistory.com
- 좌표 배율을 조정한다.
기존 x의 범위가(0, x축 최대 해상도) 이고 y의 범위가(0, y축 최대 해상도) 에서
변경 후 x의 범위가 (-ratio,ratio)이고 y의 범위가 (-1,1)이 되게 해야하며 식은 아래와 같다.
pt(배율 조정 펙터) = (2 * coord -resolution_xy) / resolution_y
- ray의 위치는 카메라 위치.
- 위에서 구한 세 벡터를 모두 더해 방향벡터를 만든다(벡터의 법칙)
비율을 위해 x와 y에는 pt를 곱해주고 z는 focal을 곱해준다.
ray dir = normalize(pt.x * cx - pt.y * cy + focal * cz)가 된다.
3. 각 픽셀에 레이를 쏴서 특정영역 표시 (구 출력)
이렇게 레이의 개념과 구성방법.
레이의 활용법중 하나인레이캐스팅 까지 이론을 알아보고 이를 토대로
shader toy에서 실제로 구현까지해 보았다.
참고 :
Ray-Tracing: Generating Camera Rays
Generating Camera Rays Reading time: 22 mins. Generating Camera Rays First, let's recall that the purpose of a renderer is to assign a color to each pixel of the frame. The result must be an accurate representation of the scene geometry as seen from a part
www.scratchapixel.com
레이캐스팅 튜토리얼 1. 레이캐스팅이 뭐야?
목차 1. 입문 레이캐스팅이 뭐야? 2. 기초 아주 기본적인 원리 (→이동) 3. 중급 예제코드로 이해하는 레이캐스터 구현 (untextured) (→이동) 4. 고급 예제코드로 이해하는 레이캐스터 구현 (textured) (
365kim.tistory.com
https://yeosong1.github.io/rt-Generating-Camera-Rays
[레이 트레이싱 : 카메라 레이 생성]
🖥 42 학습 노트 by yeosong
yeosong1.github.io
'Study > Graphics ' 카테고리의 다른 글
| ray marching 2 (0) | 2025.03.23 |
|---|---|
| ray marching 1 (0) | 2025.03.09 |
| (OpenGL) 도넛,큐브,원,사각형 그리기 (0) | 2022.11.19 |
| Chromatic Aberration 4 (색수차) (0) | 2020.12.31 |
| Chromatic Aberration 3 (색수차) (0) | 2020.12.29 |

