ray marching 4

기존 글 목록 :

https://mgun.tistory.com/5441

ray marching 1

https://mgun.tistory.com/5462

ray marching 2

https://mgun.tistory.com/5473

ray marching 3

 

첫번째 글에서는 레이마칭의 개념,

두번쨰에서는 SDF의 개념,

세번째 에서는 SDF의 활용에 대해 알아보았다.

 

이제 공간에 대해 이야기 해 보자.

view 공간에서는 카메라의 위치가 원점(0,0,0)이고 카메라는 -z방향을 바라본다.

( 그래픽스 api에 따라 z가 반대일 수 도 있음)

이 view 공간의 장점은 연산이 단순하고 직관적이라는데 있다.

모든 연산이 카메라 기준으로만 일어나도 된다면

(예를들어 ray를 통한 hit tes, 또는 샘플위치를 view 공간으로 변환해서 사용하는 경우)

view 공간에서 처리하면 된다.

하지만 월드에 존재하는 객체들과의 충돌검사나 조명계산등이

필요한 경우나, 카메라가 움직일 때도 장면이 고정되어 있어야하는 경우는 

월드 공간에서 처리해야 카메라 회전에 따른 장면이 자연스럽다.

카메라의 위치를 바꾸고 싶다면? 월드 공간으로 바꿔야 겠지.

이를 위해 해야할 일은 두가지다.

1. sphere는 어디서 보나 외형변환 체크가 어려우니까 sphere sdf가 아닌 cube sdf 사용

2. view를 world로 변환

 

1. cube sdf

- 원점에서 한변이 2인 정사각형 (cube)를 위한 sdf 사용.

https://www.shadertoy.com/view/Xtd3z7

Shadertoy

float cubeSDF(vec3 p) {
    // If d.x < 0, then -1 < p.x < 1, and same logic applies to p.y, p.z
    // So if all components of d are negative, then p is inside the unit cube
    vec3 d = abs(p) - vec3(1.0, 1.0, 1.0);
    
    // Assuming p is inside the cube, how far is it from the surface?
    // Result will be negative or zero.
    float insideDistance = min(max(d.x, max(d.y, d.z)), 0.0);
    
    // Assuming p is outside the cube, how far is it from the surface?
    // Result will be positive or zero.
    float outsideDistance = length(max(d, 0.0));
    
    return insideDistance + outsideDistance;
}

위 예제에 나오는 대로 하면 된다.

중요한 알고리즘은 이렇다.

a. d = 점과 큐브사이의 거리 (내부에 있는지, 외부에 있는지 모른다. 그냥 거리량만 체크.)

b. a에서 구한 거리량중 가장 큰 축의 값을 구한다. 

   만약 이 값이 0보다 크면 그건 표면 외부에 있는거니까 inside 값은 0, 아니면 값을 저장

c. a에서 구한 거리값이 0보다 작으면 그건 내부에 있는거니까 outside 값은 0, 아니면 값을 저장

d. 이 두 값을 더하면 내부에 있을때는 inside의 값이, 외부에 있을때는 outside값이 의미있는 값으로 되서 출력해줌.

 

2. view to world

shader toy가 glsl이다 보니 gl관련해서 look at 생각해 보자.

핵심은 카메라의 방향을 view 공간에서 world 공간으로 변환하기 위한 회전행렬을 생성해 보자.

완전한 view to world는 아니다. 

vec3 f = normalize(center - eye); // 카메라가 바라보는 전방 (forward) eye to center
vec3 s = normalize(cross(f, up)); // 오른쪽 벡터 (side)
vec3 u = cross(s, f);             // 위쪽 벡터 (recalculated up)

return mat4(
    vec4(s, 0.0),   // x축 (오른쪽)
    vec4(u, 0.0),   // y축 (위쪽)
    vec4(-f, 0.0),  // z축 (뒤쪽)
    vec4(0.0, 0.0, 0.0, 1) // 마지막 행, 원점 위치
);

이 행렬을 이용하면 view space 기준의 방향벡터를 world space로 변환할 수 있다.

완전한 변환은 마지막 행에 vec4(-dot(s, eye), -dot(u, eye), dot(f, eye), 1.0)를 넣으면 된다.

여기서는 필요없으니까 패스.

 

이렇게 다른 모양의 SDF와 view를 world로 변경해서 연산하는 이유에 대해 알아보았다.

이제 하나 이상의 SDF를 합성하는것을 알아보자.

기존에 SDF 방식은 아래 예와 같았다.

return sphereSDF(samplePoint); 이렇게 해서 구를 출력하거나,

return cubeSDF(samplePoint); 이렇게 해서 큐브를 출력하거나.

이제는 둘 다 출력해서 sphere가 cube랑 합쳐진 듯한 느낌을 출력해 보자.

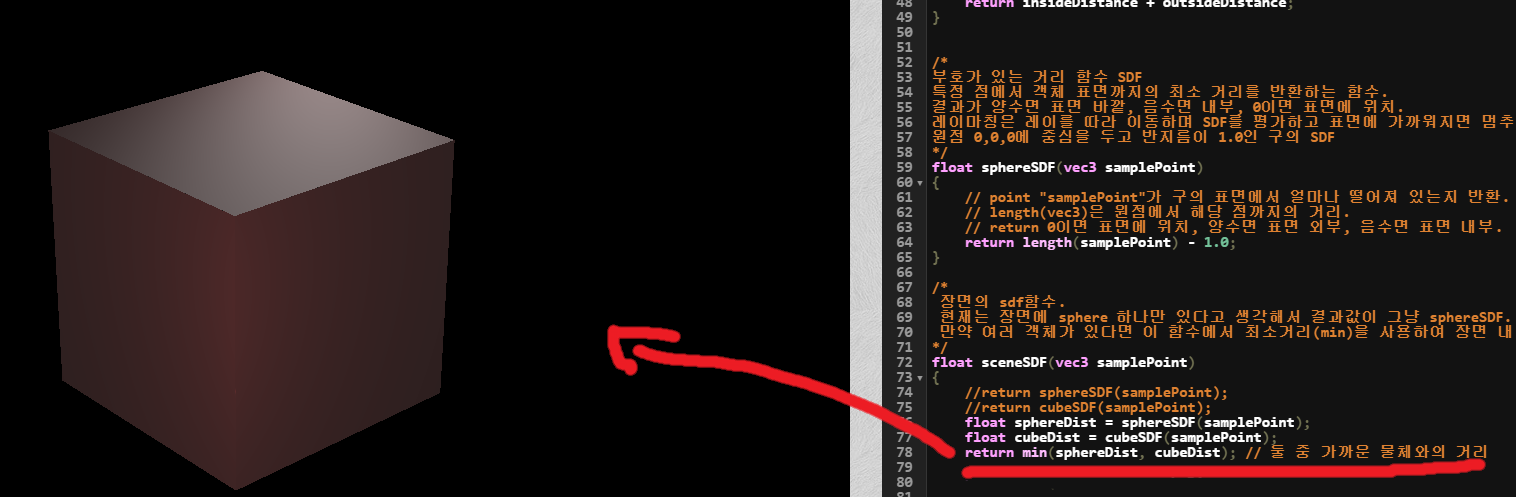
sphere와 cube의 결과값 중 min으로 출력하면 더 먼저 표면에 도달하는(가까운) 것만 체크가 되서 박스가 출력이 된다.

 

반대로 max로 출력하면 표면에 더 늦게 도달하는(멀리 있는) 것만 체크가 되서 sphere가 출력이 된다.

 

그럼 어떻게 해야 할까?

Sphere를 살짝 키워서 모서리쪽은 여전히 box가 더 커 보이고 면쪽으로는 sphere가 좀 더 커 보이게 해 보자.

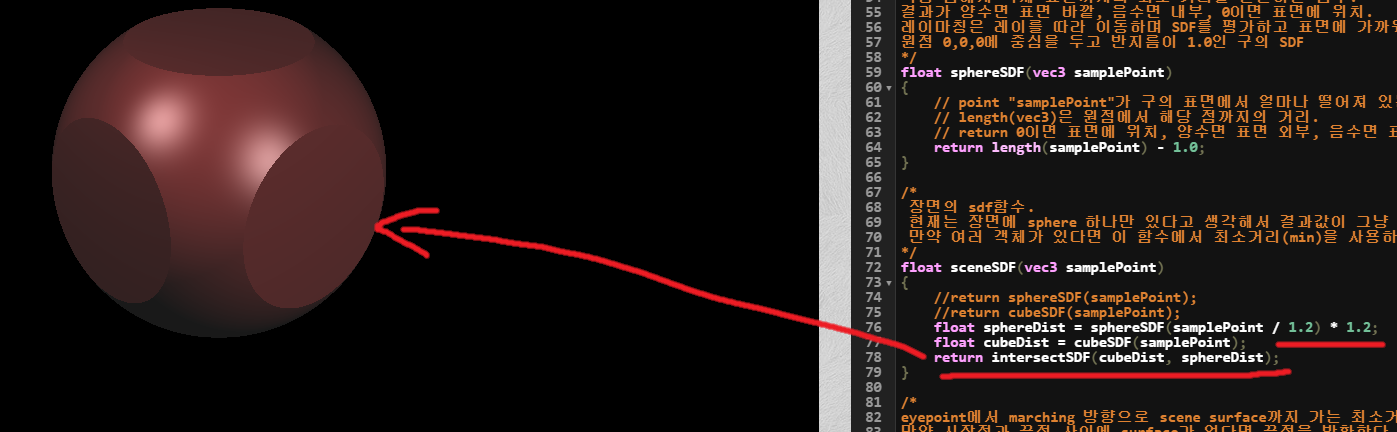
여기서 사용한 intersectSDF는 단순히 max 함수이며, 중요한 내용은 아니다.

그럼 어떤 부분이 중요한가?

위에 samplePoint를 1.2로 나누고 그 결과물을 1.2로 곱해주는것이 중요하다.

1.2로 나누기만 해도 결과는 같아보이지만 이는 올바르지 않으며 보정(스케일링 보정)이 필요하다.

아래는 이 부분에 대한 설명이다.

설명상 1.2로 하는것 보다 2로 하는게 설명이나 이해가 편해서 2 (sphereSDF(samplePoint/2.0)*2) 로 하겠다.

 

1. samplePoint를 2로 나누기 

    입력좌표를 0.5배로 축소하면, SDF입장에서는 구의 반지름은 여전히 그대로(여기서는 1) 이지만 

    원점에서의 거리가 절반으로 계산된다.

    float sphereSDF(vec3 samplePoint)
    {      
       return length(samplePoint) - 1.0;
    }

    실제 sphereSDF함수의 내부는 위와 같은데 2로 나누는건 결국 거리값 length(samplePoint)/2 -1.0 과 같다.

    이제 거리값 d가 0이 되는 지점은. length(samplePoint)/2.0 - 1 = 0 이므로 1을 넘기로 양쪽에 2를 곱하면,

     length(samplePoint) = 2가 된다. 즉, 구의 반지름이 1에서 2로 2배로 커진다.

 

2. 결과물에 2 곱하기 

    SDF함수의 핵심은 "월드 공간에서 표면까지 남은 거리"를 반환하는 것이다.

    그런데 우리는 /2를 하면서 좌표계를 반으로 축소해 보렸다.

    즉, 모든 거리가 절반 단위로 계산되는 로컬공간에 들어가 버린 것.   

단계	계산식	설명
(a) 원점에서의 실제 거리	L = length(samplePoint)	예: samplePoint = (4,0,0) 이라 하면 L = 4
(b) 좌표 축소 후 거리	L' = length(samplePoint/2.0)	(4/2, 0,0) → length = 2
(c) 로컬 SDF 반환값	d_local = sphereSDF(samplePoint/2.0) = L' - 1	반지름 1짜리 구라면, d_local = 2 - 1 = 1
(d) 월드 공간에서 남은 진짜 거리	d_world = L - 2	반지름이 2로 보이므로, 4 - 2 = 2

위 1번의 결과로 samplePoint/2를 하면 구의 반지름은 기존 1에서 2가 되어 버린다.

여기서 결과물에 2를 곱하는 보정을 안하면 어떻게 될까?

"a"를 보면 위치 p에서 원점까지의 거리는 4이며, 구의 반지름이 1이므로 4(length)-1(rid을 하여 남은 거리값은 3이 된다.

하지만 "b"와 같이 점 p를 반으로 줄이면 좌표가 줄어드는 거기 때문에 나머지도 다 반으로 줄어야 하는데,

기존 반지름 값인 1을 빼면 2(p) - 1(r)이 되어 결과는 위 "c"처럼 1이 된다.

실제로는 위 "1"번 내용에 의해 구의 반지름도 두배로 늘어서 2가 되어 있는 좌표계이며

위 "d"와 같이 줄어든 L - r(늘어난 r값)이 되어 4 - 2 = 2가 되어야 결과가 맞다.

 

여기까지 대략적인 레이마칭에 대해 다루었다.

 

레이마칭에 대해 요약해 보자면....

SDF와 함께 자주 사용되는 볼륨기반 렌더링 기법이다.

픽셀마다 레이를 발사해서 물체와의 충돌을 반복적으로 추정하며 접근하는 방식이다.

1. 카메라에서 각 픽셀방향으로 레이를 발사

2. 현재 위치에서 가장 가까운 물체까지의 거리 계산(SDF), 이 거리만큼 앞으로 나아가도

     어떤 물체와도 충돌하지 않으므로 한번에 많이 이동 가능.

3. 측정된 거리가 아주 작아지면 충돌한 것으로 간주하고, 그렇지 않다면 그 거리만큼 전진 반복.

4. 최대 반복횟수나 최대거리 초과시까지 아무것도 만나지 못했다면 배경색으로 처리.

 

SDF는 쉽게말해...

모델링 대신 수학적으로 물체를 정의할 수 있다.

예를들어 여태까지 사용했던 sphere sdf나 cube sdf 같은거.

그리고 여러 sdf를 결합해서 새로운 형태도 제작할 수 있다.

보통 최대 횟수를 줄이기 위해 Bounding Volume, Distance Field Optimization, Level Of Detail등을 활용한다.

SDF를 기반으로 Surface Normal, Soft Shadow, AO, Reflection등도 구현 가능하다.